Deleting a node is the hardest part of implementing an RB-Tree. Let’s write a helper function that moves the parent of node U to node V. This function is called “Transplant”. We will also use another helper function to get the least node in a sub-tree.
void transplant(RBNode* u, RBNode* v)
{
if(u->m_parent == &sentinel) { root = v; }
else if(u->m_parent->m_left == u) { u->m_parent->m_left = v; }
else { u->m_parent->m_right = v; }
v->m_parent = u->m_parent;
}
RBNode* getMinimumInSubTree(RBNode* node)
{
RBNode* current = node;
while(current->m_left != &sentinel)
{
current = current->m_left;
}
return current;
}
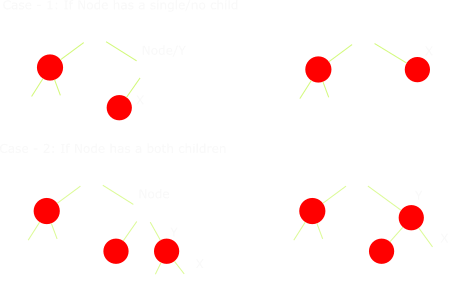
When deleting, we keep track of the color of node that’s being deleted and also a node(X) that takes the place of the node that’s being deleted, which might introduce violations. And, 2 things must be considered when deleting a node:
– If node has a single/no child. In this case, we store the original color of this node and make left/right child or sentinel take the node’s place.
– If node has 2 valid children, we get the least node in the right sub-tree(Y) and have that replace the node being deleted. During this operation, there should be another node that takes Y’s place. That will be Y->Right, our X in this case. Here, we keep track of Y’s(successor ) original color.
Once we delete the node, we call a DeleteFixup function if the original color of deleted node is BLACK.
void remove(RBNode* node)
{
RBNode* y = node;
bool yOriginalColorIsRed = y->m_isRed;
RBNode* x = &sentinel;
if(node->m_left == &sentinel)
{
x = node->m_right;
transplant(node, node->m_right);
}
else if(node->m_right == &sentinel)
{
x = node->m_left;
transplant(node, node->m_left);
}
else
{
//Node has 2 valid children
y = getMinimumInSubTree(node->m_right);
yOriginalColorIsRed = y->m_isRed;
// we color Y the same color as z.
// y->right take's Y's place.
x = y->m_right;
//Node being deleted is not immediate parent of Y.
if(y->m_parent == node)
{
//This check is for sentinel. If y has no children, we store the parent info in sentinel
x->m_parent = y;
}
else
{
//Move X To Y's place
transplant(y, x);
y->m_right = node->m_right;
y->m_right->m_parent = y;
}
//Move Y To Z'a Place and take it's color
transplant(node, y);
y->m_left = node->m_left;
node->m_left->m_parent = y;
y->m_isRed = node->m_isRed;
}
if(!yOriginalColorIsRed){ RBDeleteFixup(x); }
}
Delete-Fixup:
Once deleted, we could have following violations:
– If the delete node is root, then the node that replaces it might be RED.
– If the node replacing could be a RED node and it’s parent could also be RED.
– The number of black nodes in any simple path might not be equal anymore.
To fix the third scenario, we introduce “Double Blackness” and “Red/Black”. If the node that replaces the deleted node is BLACK/RED, the sub-tree would be deficit by one black node. If the replacing node is BLACK, then it would be “Double Black”, and “RED-BLACK” otherwise.

Double-Black and Red-Black are kind of abstract properties. They dont need to be represented as data in code. Now that we have established that, let’s look at the Delete Fixup scenarios. Here, I assume the node under focus is left child and “Sibling” is a right child. We are looking at 4 cases here:
1. If sibling is RED, it must mean that our parent is BLACK. We can switch colors of Sibling to BLACK and parent to RED and perform Left Rotation on parent and update the Sibling’s pointer. The might not fix the violations introduced, but it transforms the problem in a way that ensures sibling is BLACK and will be handled by following cases.
2. If sibling is BLACK and both it’s children are also BLACK. This case is simple. We just color sibling RED and make the active node as our current parent. Since we have an Double-Blackness on the left subtree, making sibling RED will make it lose a black node, thereby balancing both sub-trees.
3. If sibling is BLACK and it’s left child is RED. We color sibling RED and it’s left child to BLACK and perform RightRotation on sibling to convert this to Case 4. This might not fix the violations, but leads into Case-4
4. If sibling is BLACK and it’s right child is RED, sibling takes the color of it’s parent and parent is made RED and LeftRotation is performed on Parent. Now, the left sub-tree will have an additional black node, fixing the violation.
Hope this helped! Please like the posts if you’ve learnt something. Really boosts the motivation and drive to post more content.
Here’s the Code Snippet
void RBDeleteFixup(RBNode* node)
{
while(node != root && !node->m_isRed)
{
if(node->m_parent->m_right == node)
{
//Uncle should always be present
RBNode* sibling = node->m_parent->m_left;
if(sibling->m_isRed)
{
sibling->m_isRed = false;
sibling->m_parent->m_isRed = true;
RightRotate(sibling->m_parent);
sibling = node->m_parent->m_left;
}
//Case - 2: Uncle is black and Left and right children of uncle are null or red
if(sibling == &sentinel || (!sibling->m_left->m_isRed && !sibling->m_right->m_isRed))
{
if(sibling != &sentinel)
{
sibling->m_isRed = true;
}
// Extra blackness is added to parent, making in RB or BB to compensate for removing
// a black on uncle and node
node = node->m_parent;
}
else
{
//Uncle's right is red, transform to make both left and right as black
if(sibling->m_right->m_isRed)
{
sibling->m_right->m_isRed = false;
sibling->m_isRed = true;
LeftRotate(sibling);
sibling = node->m_parent->m_left;
}
sibling->m_isRed = node->m_parent->m_isRed;
node->m_parent->m_isRed = false;
sibling->m_left->m_isRed = false;
RightRotate(node->m_parent);
node = root;
}
}
else
{ //Same as previous block with Left and Right exchanged}
}
node->m_isRed = false;
}
