Introduction
Quick sort is definitely quite an efficient algorithm and is quite efficient if size of data set is low or moderate. That is why I decided it’s worth exploring how it performs under a multi-threaded scenario. While going through “Concurrency In Action” by Anthony Williams(Amazing read btw!!), I had quite some trouble implementing the example presented in Listing 8.1. The basic idea of that implementation was that the “right” recursion step(pivot to last element) of quick sort algorithm was submitted as a batch for any thread to pick up. It is also free to take any work that’s already submitted while it waits for result from other threads.
This quickly went out of hand and my code started exceeding stack limits. So, I went on an expedition to find a clue on how to implement a Parallel Quick Sort and came across this paper and was able to wrap my head around “Shared-Address-Space Parallel Formulation” and decided to give it a shot!
With this algorithm, I was able to achieve speeds nearly ~3-8x faster than serial quick-sort. Speed largely depends on the number of threads we are using and how the elements are finally split into batches. There would be a decrease in performance if all batches are not roughly of same size.
Serial Quick Sort
Quick sort is a Divide and Conquer algorithm. We split the problem into smaller chunks, solve them and combine. Before working on our parallel algorithm, let’s first break down what’s happening in a serial quick sort in following points:
- We have an input Array(A) of size N, the first and last indices of elements that should be sorted.
- We calculate a pivot element in the array. To make things simple, this can just be the starting element in the array provided.
- Using this pivot, we divide (A) into 2 parts. Left half will have elements smaller than (A) and right half will have elements greater than or equal to (A).
- We repeat the step above until (first <= last) and then the function returns.
- Once the function returns, it would already have sorted the sub array perfectly and no additional step for merging the arrays is required.
void doSortSerial(int first, int last, int* data)
{
numRecursion.fetch_add(1);
if(first >= last)
{
return;
}
//First element is our pivot;
int index = first;//std::rand() % (last - first);
int pivot = data[index];
//Split at pivot
int pivotPos = first;
for(int i = first + 1; i <= last; i++)
{
if(data[i] < pivot)
{
//Exchange data with pivot pos
++pivotPos;
int temp = data[i];
data[i] = data[pivotPos];
data[pivotPos] = temp;
}
}
//Exchange pivot with beginning element
data[first] = data[pivotPos];
data[pivotPos] = pivot;
doSortSerial(first, pivotPos - 1, data);
doSortSerial(pivotPos + 1, last, data);
}
Understanding Parallel Implementation
Now that the obvious is out of the way, let’s try and understand what it means to parallelize an algorithm. In it’s simplest essence, parallelizing an algorithm is taking advantage of multiple processors and split the work we are given equally in hopes of achieving an increase in computation speed in proportion to number of processors we have dedicated for the problem.
What if we split the array we are given into uniform chunks and make each thread take care of sorting that particular chunk? Well, that was my initial thought track and there’s one obvious problem with this approach, which is depicted below:

If the problem is not already obvious, if we naively split the given array into multiple chunks and perform quick sort on them, the individual chunks would be sorted, but there’s no guarantee that the entire array would be!
There is a way to make this work if we put in some additional guidelines. The main problem is that, when we split the array arbitrarily, there isn’t any rule imposed on which elements should go into which part of the array. Therefore, we can end up with elements in left split that are greater than elements in right split and vice versa.
Therefore, we need to impose a rule asking all elements smaller than a certain value to take up the left split and elements that are greater to take up the right split. This would let us sort multiple chunks of array parallelly and the final array would just be a combination of all the chunks.
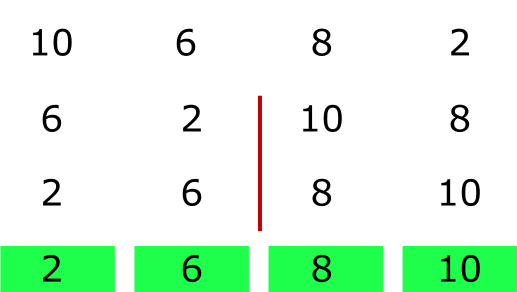
This is the overall idea of how to parallelize quick-sort. There are a few steps from the paper I glossed over, which I’ll enumerate in the subsequent sections. But, we can now formulate a strategy to parallelize our quick sort!!
Parallel Quick Sort: getting Ready
Algorithm can be broken down into following steps:
- We have an input Array(A) of size N, the first and last indices of elements that should be sorted.
- We decide the number of threads(T) on which algorithm is going to run.
- Input array is initially split into 1 “Group” with T “Batches”. Each batch runs on a separate thread, so a data race would be impossible.
- A Group is a collection of batches and contains a “Key” that’s used for segregating the batches that fall into the group.
- Elements in a batch are split into 2 parts based on Group’s key. Left part contains elements smaller than key and right half contains elements that are greater. Each batch runs on it’s own thread.
- Once we have split the individual batches based on group’s key, we now need to split elements in the entire group based on the same key. This can be done with the help of prefix sum arrays and an auxiliary array.
- The group is now split into two and steps 3 – 7 are repeated until number of groups becomes equal to the number of threads(T).
- Once Groups becomes equal to Threads, we would’ve split the input array in such a way that elements in left batch are always less than the elements in the right batch. Therefore, serial quick sort can now be performed on (T) individual batches to get the final sorted array.
Before implementing the algorithm, let’s define a few things that lets us easily split the work across threads. I created a naïve Function Wrapper that lets me store a function with arguments that I want to call and is easily accessible by all the threads. This is completely optional and you could go with any other way for submitting work to threads. All of the code will reside in the class Parallel_Quicksort.
const int numThreads = 8;
class Parallel_Quicksort
{
enum class State
{
Initializing,
Working,
WorkReady,
Done,
};
struct FunctionWrapperBase
{
void invoke()
{
valid = false;
callback();
}
protected:
std::function<void()> callback;
bool valid = false;
};
template<typename T, typename OBJECT, typename ...PARAM>
struct FunctionWrapper : public FunctionWrapperBase
{
FunctionWrapper(){};
FunctionWrapper(T func, OBJECT object, PARAM... param)
{
callback = [func, object, param...](){
(object->*func)(param...);
};
valid = true;
}
};
template <typename T, typename ...PARAM>
struct FunctionWrapper<T, nullptr_t, PARAM...> : public FunctionWrapperBase
{
FunctionWrapper(T func, PARAM... param)
{
callback = [func, param...](){
(*func)(param...);
};
valid = true;
}
};
template<typename T, typename OBJECT, typename ...PARAM>
static FunctionWrapper<T,OBJECT, PARAM...> createWrapper(T func, OBJECT object, PARAM... param)
{
return FunctionWrapper<T,OBJECT, PARAM...>(func, object, param...);
}
template<typename T, typename ...PARAM>
static FunctionWrapper<T, nullptr_t, PARAM...> createGlobalWrapper(T func, PARAM... param)
{
return FunctionWrapper<T, nullptr_t, PARAM...>(func, param...);
}
struct Work
{
Work() : done(true) {}
Work(FunctionWrapperBase work)
{
wrapper = work;
done = false;
}
void doWork()
{
done = false;
wrapper.invoke();
done = true;
}
FunctionWrapperBase wrapper;
bool done = true;
};
void run(int id)
{
while(state != State::Done)
{
std::this_thread::yield();
doWork(id);
}
}
void doWork(int id)
{
if(!workBatches[id].done)
{
workBatches[id].doWork();
updateWork();
}
}
void updateWork()
{
bool done = true;
for(Work& work : workBatches)
{
done &= work.done;
}
if(done)
{
state = State::WorkReady;
}
}
void waitForWork()
{
while(state == State::Working)
{
std::this_thread::yield();
}
}
Parallel Quick Sort: Implementation
Let’s first define two really important structures: Group and Batch. To re-iterate, a group is a collection of batches and a Batch is a portion of input array that is run on a dedicated thread.
In the code below, lowerDistMedian and upperDistMedian are used for calculating Key of the group so that elements can be split uniformly when quick sort is performed on each batch. Batch ID corresponds with the thread ID that this batch is supposed to run on.
We then start off the algorithm by calling “doSortParallel”, which creates batches containing start and end of indices of elements in the array that this batch would operate on. An auxiliary array “tmpData” is also created to help us with global re-arrangement of data.
struct Batch
{
int id = -1;
int start = -1;
int end = -1;
bool batchReady = false;
size_t lowerDistMedian = 0;
size_t upperDistMedian = 0;
};
struct Group
{
std::vector<Batch> batches = std::vector<Batch>();
int key = -1;
int start = -1;
int end = -1;
std::vector<int> lowerElemPrefixSum;
std::vector<int> higherElemPrefixSum;
};
void doSortParallel(int first, int last, int* data)
{
size_t numElements = (last - first) + 1;
int elementsPerBatch = numElements/numThreads;
int excess = numElements % numThreads;
workBatches.resize(numThreads);
std::vector<Batch> batches(numThreads);
int current = 0;
for(int i = 0; i < numThreads; i++)
{
Batch batch;
int numElements = elementsPerBatch;
if(excess != 0)
{
--excess;
++numElements;
}
batch.id = i;
batch.start = current;
current += numElements;
batch.end = current - 1;
batches[i] = batch;
}
Group group;
group.batches = batches;
group.start = first;
group.end = last;
// Assuming elements are [0, maxElementsNum), key is selected as mid point for uniform distribution
group.key = numElements / 2;
group.lowerElemPrefixSum.resize(batches.size() + 1);
group.higherElemPrefixSum.resize(batches.size() + 1);
groups.push_back(group);
size_t size = numElements * sizeof(int);
int* tmpData = (int*)malloc(size);
memcpy(tmpData, data, size);
//Start Threads
for(size_t i = 1; i < numThreads; i++)
{
threads[i-1] = std::thread(&Parallel_Quicksort::run, this, i);
}
doSortParallel_Impl(first, last, data, tmpData);
free(tmpData);
}
To split elements in a batch based on group’s key, we employ the same technique as in quick sort algorithm by splitting elements based on a pivot. While going through each element in a batch, we keep track of the highest and lowest element of the two halves and store a median value for better key calculation when groups are split!
Once elements are split locally in their respective batches, they must be re-arranged so that all the elements of the group are now split based on the key. This is the global rearrangement step and is done with the help of prefix Sum computations. The code for the two operations is as follows:
//This sorts data in the temp data batch
//Happens in parallel
void sortBatch(Group& group, int batchIndex, int* tmpData)
{
Batch& batch = std::ref(group.batches[batchIndex]);
int dataSize = batch.end - batch.start + 1;
if(dataSize < 2)
{
return;
}
//An expensive operation
int swapPos = batch.start;
int numLowerHalf = 0;
int minLower = INT32_MAX; int maxLower = 0;
int minUpper = INT32_MAX; int maxUpper = 0;
for(int i = batch.start; i <= batch.end; i++)
{
if(tmpData[i] < group.key)
{
if(tmpData[i] < minLower)
{
minLower = tmpData[i];
}
if(tmpData[i] > maxLower)
{
maxLower = tmpData[i];
}
int temp = tmpData[i];
tmpData[i] = tmpData[swapPos];
tmpData[swapPos] = temp;
++swapPos;
++numLowerHalf;
}
else
{
if(tmpData[i] < minUpper)
{
minUpper = tmpData[i];
}
if(tmpData[i] > maxUpper)
{
maxUpper = tmpData[i];
}
}
}
batch.lowerDistMedian = (minLower + maxLower) / 2;
batch.upperDistMedian = (minUpper + maxUpper) / 2;
group.lowerElemPrefixSum[batchIndex] = numLowerHalf;
group.higherElemPrefixSum[batchIndex] = dataSize - numLowerHalf;
}
//Happens in parallel.
void mergeSortedWithOriginal(Group& group, int batchIndex, int* data, int* tmpData)
{
int start = group.start;
Batch& batch = group.batches[batchIndex];
int pos = start + group.lowerElemPrefixSum[batchIndex];
size_t size = group.lowerElemPrefixSum[batchIndex + 1] - group.lowerElemPrefixSum[batchIndex];
int dataSize = sizeof(data[0]);
memcpy((void*)(data + pos), (void*)(tmpData + batch.start), size * dataSize);
int initial = size;
pos = start + group.higherElemPrefixSum[batchIndex];
size = group.higherElemPrefixSum[batchIndex + 1] - group.higherElemPrefixSum[batchIndex];
memcpy((void*)(data + pos), (void*)(tmpData + batch.start + initial) , size * dataSize);
}
After global re-arrangement, we have a group with elements that are clearly split on the given key. We then split the group into two. First group contains all the elements that are smaller than the key and the second group contains all the elements that are larger than the key.
To make things simple, batches are equally split between the two new groups and we use prefix sum arrays to calculate distribution of elements. This is how it’s done:
void splitGroups()
{
//This should be quite a trivial operation. Loops groups * batches times
std::vector<Group> newGroups;
for(size_t i = 0; i < groups.size(); i++)
{
//split a group based on key if it has multiple batches
size_t numBatches = groups[i].batches.size();
int currentLowerPos = groups[i].start;
int currentHigherPos = currentLowerPos + groups[i].higherElemPrefixSum[0];
if(groups[i].batches.size() > 1)
{
int firstGroupBatches = groups[i].batches.size() / 2;
int secondGroupBatches = groups[i].batches.size() - firstGroupBatches;
std::vector<int> lowerElements;
std::vector<int> higherElements;
Group g1 = Group();
g1.start = groups[i].start;
Group g2 = Group();
g2.start = currentHigherPos;
g2.end = groups[i].end;
int numLowerHalfElements = groups[i].lowerElemPrefixSum[numBatches];
int elementsPerBatch = numLowerHalfElements / firstGroupBatches;
int excess = numLowerHalfElements % firstGroupBatches;
int key = 0;
for(int j = 0; j < firstGroupBatches; j++)
{
//Move batches from G. This retains the ID information
g1.batches.push_back(groups[i].batches[j]);
int elementsInBatch = elementsPerBatch;
if(excess)
{
++elementsInBatch;
--excess;
}
int endPos = currentLowerPos + elementsInBatch - 1;
g1.batches[j].start = currentLowerPos;
g1.batches[j].end = endPos;
g1.end = endPos;
key += g1.batches[j].lowerDistMedian;
g1.batches[j].lowerDistMedian = 0;
currentLowerPos += elementsInBatch;
}
g1.key = key / firstGroupBatches;
int numHigherHalfElements = groups[i].higherElemPrefixSum[numBatches] - numLowerHalfElements;
elementsPerBatch = numHigherHalfElements / secondGroupBatches;
excess = numHigherHalfElements % secondGroupBatches;
key = 0;
for(int j = 0; j < secondGroupBatches; j++)
{
int batchIndex = firstGroupBatches + j;
g2.batches.push_back(groups[i].batches[batchIndex]);
int elementsInBatch = elementsPerBatch;
if(excess)
{
++elementsInBatch;
--excess;
}
int endPos = currentHigherPos + elementsInBatch - 1;
g2.batches[j].start = currentHigherPos;
g2.batches[j].end = endPos;
key += g2.batches[j].upperDistMedian;
g2.batches[j].upperDistMedian = 0;
currentHigherPos += elementsInBatch;
}
g2.key = key / secondGroupBatches;
g1.lowerElemPrefixSum.resize(g1.batches.size() + 1);
g1.higherElemPrefixSum.resize(g1.batches.size() + 1);
g2.lowerElemPrefixSum.resize(g2.batches.size() + 1);
g2.higherElemPrefixSum.resize(g2.batches.size() + 1);
if(g1.batches.size() > 0)
{
newGroups.push_back(g1);
}
if(g2.batches.size() > 0)
{
newGroups.push_back(g2);
}
}
if(groups[i].batches.size() == 1)
{
newGroups.push_back(groups[i]);
}
}
groups = newGroups;
}
Finally, tying it all together is our main implementation function, which performs following steps:
- Loops through groups and
- submits each batch to split elements locally if no. of groups is not equal to no. of threads.
- submits each batch to perform quick sort if no. of groups is equal to no. of threads.
- Waits for (1) to complete. If groups is equal to no. of threads here, we would’ve performed quick sort and the function returns.
- Calculates prefix sums of lower and upper half elements of all the batches in the group and stores in its respective group.
- Performs global re-arrangement step. The portion of original array that group is operating on is modified to contain elements that are split based on the key. This is a parallel operation.
- Waits for (4) to complete.
- Finally current groups are iterated and split into two with the help of prefix sum arrays. One of the new groups contains all the elements that are lower than the key and the other contains elements that are greater!
void doSortParallel_Impl(int first, int last, int* data, int* tmpData)
{
for(size_t i = 0; i < groups.size(); i++)
{
if(groups[i].batches.size() == 0)
{
continue;
}
// Start running all groups at once on each thread.
// Wastes time if run before groups size becomes equal to numThreads
if(groups[i].batches.size() == 1 && groups.size() == numThreads)
{
if(groups[i].batches[0].batchReady)
{
continue;
}
//In Serial sort, eveything is sorted in lower batch step
int dataSize = groups[i].batches[0].end - groups[i].batches[0].start + 1;
groups[i].lowerElemPrefixSum[0] = dataSize;
groups[i].higherElemPrefixSum[0] = 0;
state = State::Working;
auto wrapper = createWrapper(&Parallel_Quicksort::doSortSerial, this,
groups[i].batches[0].start, groups[i].batches[0].end, data);
workBatches[groups[i].batches[0].id] = Work(wrapper);
groups[i].batches[0].batchReady = true;
}
else
{
//Check if batches are greater than number of threads and bail out
int size = groups[i].batches.size();
for(size_t j = 0; j < groups[i].batches.size(); j++)
{
if(groups[i].batches[j].start >= groups[i].batches[j].end)
{
continue;
}
state = State::Working;
auto wrapper = createWrapper(&Parallel_Quicksort::sortBatch, this, std::ref(groups[i]), j, tmpData);
workBatches[groups[i].batches[j].id] = Work(wrapper);
}
}
}
doWork(0);
waitForWork();
if(groups.size() == numThreads)
{
state = State::Done;
return;
}
//Calculate Prefix sums in respective groups
for(size_t i = 0; i < groups.size(); i++)
{
int prevValue = groups[i].lowerElemPrefixSum[0];
groups[i].lowerElemPrefixSum[0] = 0;
int totalLower = 0;
for(size_t j = 1; j < groups[i].lowerElemPrefixSum.size(); j++)
{
int oldLower = prevValue;
prevValue = groups[i].lowerElemPrefixSum[j];
groups[i].lowerElemPrefixSum[j] = groups[i].lowerElemPrefixSum[j - 1] + oldLower;
totalLower = groups[i].lowerElemPrefixSum[j];
}
prevValue = groups[i].higherElemPrefixSum[0];
groups[i].higherElemPrefixSum[0] = totalLower;
for(size_t j = 1; j < groups[i].higherElemPrefixSum.size(); j++)
{
int oldHigher = prevValue;
prevValue = groups[i].higherElemPrefixSum[j];
groups[i].higherElemPrefixSum[j] = groups[i].higherElemPrefixSum[j - 1] + oldHigher;
}
}
for(size_t i = 0; i < groups.size(); i++)
{
for(size_t j = 0; j < groups[i].batches.size(); j++)
{
int dataSize = groups[i].batches[j].end - groups[i].batches[j].start + 1;
if(dataSize == 0)
{
continue;
}
state = State::Working;
auto wrapper = createWrapper(&Parallel_Quicksort::mergeSortedWithOriginal,
this, std::ref(groups[i]), j, data, tmpData);
workBatches[groups[i].batches[j].id] = Work(wrapper);
}
}
doWork(0);
waitForWork();
size_t size = (last - first + 1) * sizeof(int);
memcpy(tmpData, data, size);
splitGroups();
doSortParallel_Impl(first, last, data, tmpData);
}
That’s all folks! Hope you got to learn something 🙂
